CONNECT BY and Recursive CTE

11gR2 introduced a new mechanism to build up hierarchies.

I remembered a thread in developpez.net that reveals the dubious implementation of nocycle in 10g.

For the CONNECT BY ISLEAF, I have read the technique on amis.nl.

Ok, here is my graph

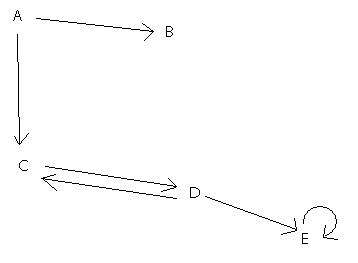
The 10g query

with o as
(
SELECT 'A' obj, 'B' link from dual union all
SELECT 'A', 'C' from dual union all
SELECT 'C', 'D' from dual union all
SELECT 'D', 'C' from dual union all
SELECT 'D', 'E' from dual union all
SELECT 'E', 'E' from dual)
select connect_by_root obj root,level,obj,link,
sys_connect_by_path(obj||
'->'
||link,','),
connect_by_iscycle,
connect_by_isleaf
from o
connect by nocycle obj=prior link
start with obj='A';

ROOT LEVEL O L PATH CYCLE LEAF
---- ----- - - -------------------- ----- -----
A 1 A B ,A->B 0 1
A 1 A C ,A->C 0 0
A 2 C D ,A->C,C->D 1 0
A 3 D E ,A->C,C->D,D->E 1 1


Obviously in 10g the connect by nocycle does not work that well with that kind of graphs, D-C and E-E are missing and C-D and D-E are marked as cycling…

Let’s try the 11gR2 equivalency.

with o(obj,link) as
(
SELECT 'A', 'B' from dual union all
SELECT 'A', 'C' from dual union all
SELECT 'C', 'D' from dual union all
SELECT 'D', 'C' from dual union all
SELECT 'D', 'E' from dual union all
SELECT 'E', 'E' from dual),
t(root,lev,obj,link,path) as (
select obj,1,obj,link,cast(obj||'->'||link
as varchar2(4000))
from o
where obj='A' -- START WITH
union all
select
t.root,t.lev+1,o.obj,o.link,
t.path||', '||o.obj||
'->'
||o.link
from t, o
where t.link=o.obj
)
search depth first by obj set ord
cycle obj set cycle to 1 default 0
select root,lev,obj,link,path,cycle,
case
when (lev - lead(lev) over (order by ord)) < 0 then 0 else 1 end is_leaf from t; ROOT LEV OBJ LINK PATH CYCLE IS_LEAF ---- ---- ---- ---- --------------------------- ----- ------- A 1 A B A->B 0 1
A 1 A C A->C 0 0
A 2 C D A->C, C->D 0 0
A 3 D C A->C, C->D, D->C 0 0
A 4 C D A->C, C->D, D->C, C->D 1 1
A 3 D F A->C, C->D, D->E 0 0
A 4 F F A->C, C->D, D->E, E->E 0 0
A 5 F F A->C, C->D, D->E, E->E, E->E 1 1


It looks good 🙂

If you exclude the rows with cycle=1, you get the six rows for the graph.